Ionization Energies of Para-H2 from Zero-Quantum-Defects Positions
From the precise measurement of the ionization energy of H2 its dissociation energy can be determined [1], which serves as a benchmark quantity for QED calculations [2]. Additionally, measurements of ionization energies corresponding to higher rovibrational levels of the ion enable the determination of rovibrational intervals in H2+ [3]. These intervals can be calculated extremely precisely for one-electron systems, offering the prospect of improving the value of fundamental constants or particle properties such as the proton-to-electron mass ratio [4]. Until now, the most precise determinations of the ionization energies of molecular hydrogen have relied on the extrapolation of Rydberg series using multichannel quantum-defect theory (MQDT) [5]. These extrapolations are typically accurate to less than 500 kHz, currently representing the dominant source of uncertainty in the determinations of ionization energies. Additionally, autoionization lifetimes restrict mmW measurements to states below the lowest ionization threshold which renders accurate extrapolations to higher rovibrational levels of the ion difficult.
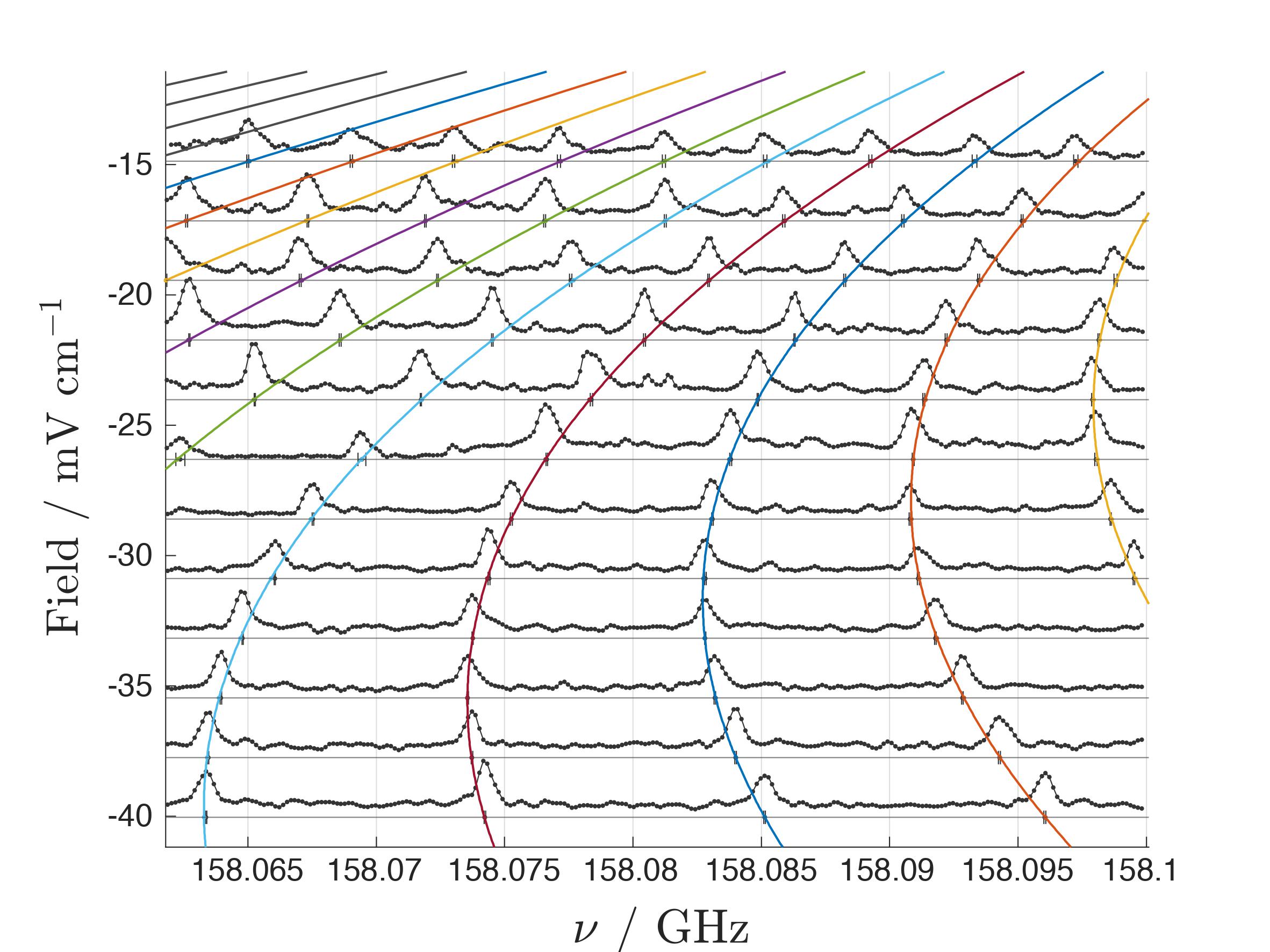
We present here a method to determine the binding energies of Rydberg states without having to resort to a Rydberg-series extrapolation. We carry out precision measurements of the linear Stark manifolds associated with near-degenerate high-l states by mmW spectroscopy in the presence of intentionally applied electric fields. Extrapolating the linear Stark manifold to zero field yields accurate values of the zero-quantum-defect positions, given by -RH2/n2 relative to the ionization thresholds. This circumvents the current bottlenecks and opens a route for order-of-magnitude improvements of the ionization energies in molecular hydrogen.
[1] N. Hölsch, et al., Phys. Rev. Lett., 2019, 122(10), 103003
[2] M. Puchalski, et al., Phys. Rev. Lett., 2019, 122(10), 103003
[3] C. Haase, et al., J. Chem. Phys., 2015, 142(6), 064310
[4] I.V. Kortunov, et al., Nat. Phys., 2021, 1-5
[5] D. Sprecher, et al., J. Chem. Phys., 2014, 140, 104303:1-18