Relativistic and QED corrections for precision spectroscopy: state of the art and beyond
The quantitative understanding of high-precision molecular spectra requires the accurate computation of effects beyond the well-known non-relativistic Born–Oppenheimer picture. Few-electron molecules with low nuclear charge are of interest of both experimental and theoretical precision spectroscopy. The experiments together with theoretical computations are proposed as tests of our fundamental understanding of ordinary matter in the low-energy range. The underlying theory of the electromagnetic interactions, quantum electrodynamics (QED), can be applied in the computation of highly accurate rovibronic transitions. The non-relativistic QED (nrQED) framework allows us to include higher-order relativistic and radiative processes as corrections to the Schrödinger equation. In this contribution, applications of nrQED is presented for the rovibrational intervals in the EF 1∑g+ excited electronic state of the hydrogen molecule and the rovibrational intervals of the 4He2+ molecular ion in its gorund electronic state [1]. In both cases, the agreement of the experimental transitions with the latest theoretical results was improved by several orders of magnitude [2,3]. The different contributions from the non-adiabatic, relativistic and QED corrections reveal an interesting interplay of the underlying physical phenomena.
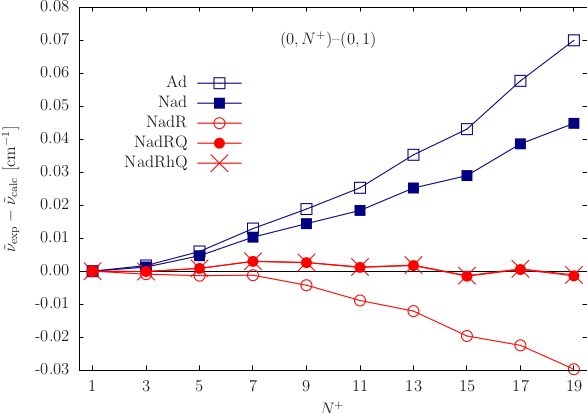
Despite the excellent agreement for low-Z molecules there is still room for improvement on the theoretical side. The nrQED fails for molecules with medium and high nuclear charge, and the computation of higher-order correction terms is an increasingly complex numerical task. An alternative approach could be formulated by the solution of the Dirac–Coulomb(–Breit) equation by treating the relativistic and correlation effects on an equal footing [4]. The applicability of the method is not limited to low-Z species and it might serve as a complementary or possibly a competitive approach to nrQED.
[1] D. Ferenc, E. Mátyus, Phys. Rev. Lett., 2020, 125, 213001; Phys. Rev. A, 2019, 100, 020501(R).
[2] L. Semeria, P. Jansen, G. Camenisch, F. Mellini, H. Schmutz, F. Merkt, Phys. Rev. Lett., 2020, 124, 213001.
[3] G. D. Dickenson, E. J. Salumbides, M. Niu, Ch. Jungen, S. Ross, W. Ubachs., Phys. Rev. A, 2012, 86, 032502.
[4] P. Jeszenszki, D. Ferenc, E. Mátyus, J. Chem. Phys., 2021, 154, 224110.